numeri

So I decided to start my own JavaScript numerical library, and I called it numeri. Here is its github.

There are a lot of good numerical libraries already out there, in languages like Python, C++, Julia, and R. These make many operations simple to code and fast to run:

• add two vectors
• do a matrix multiplication
• work with n-dimensional tensors
• get the eigenvalues and eigenvectors of a matrix

But I've never been satisfied with any such library for web (namely JavaScript). Here are my complaints with some notable ones:

• mathjs doesn't do complex operations and is slow for things like matrix multiplication.
• gl-matrix doesn't do n-dimensional tensors or even arbitrarily-sized vectors and matrices. It doesn't support many complex operations. Also, it has a lot of repetitive code.
• blasjs has extremely difficult syntax and no complex operations.
• ml-matrix doesn't do n-dimensional tensors. Also, its code is somewhat unfortunate, with a different class for every possible type of view.

Numeri currently supports n-dimensional tensors, unary operators like negation (in-place or otherwise), binary operators like addition (in-place or otherwise), slicing, reshaping, transposition, matrix multiplication, broadcasting, some simple reductions like sum, and eigenvalue/eigenvectors for symmetric matrices.

Oh yeah, and it's package size might grow a bit, but is wonderfully small, great for putting in a web page. Here it is on a log scale:

It's not without limitations, though - it currently only supports dense, real-valued tensors. I also have yet to build in the myriad of nonlinear operations remaining like matrix inversion.

Here are some of the decisions I made and tricks I learned when creating numeri.

Arrays: nested or flat?

Consider the two following options for storing the matrix

• Nested arrays; {data: [[1, 2, 3], [4, 5, 6]]}
• Single array with shape; {data: [1, 2, 3, 4, 5, 6], shape: [2, 3]}

The latter is used in numeri and every good numerical library I know of, but the choice might not be immediately obvious.

Initially the first option seems a bit more intuitive and allows for constant-time row slices. If you want to get the 0th row, you can just return {data: myTensor.data[0]}.

However, the first option requires substantially more space per tensor. A 1000x1x1 tensor in this format would require 2001 arrays to store only 1000 numbers. Also, iterating over all entries of a nested array structure is a pain, and computationally slow. Since we want to support n-dimensional tensors, one would need to recurse through each dimension of nested arrays to access all elements. This would both make the code complicated and increase runtime for basic operations.

I'll show in the next section how we can do constant-time row (and column!) slices using the 2nd option anyway.

Constant-time slicing and reshaping: probably choose one

Having chosen to represent a tensor as a flat array with some metadata like shape, there's actually some freedom to make some frequent tensor operations run in constant time. We can do this by making these operations return a view, pointing to the same data array, but using more metadata. Views behave exactly like usual tensors, except that a change to its data will affect the original tensor and any other view of that tensor, and that accessing their elements can be slower since their data isn't always contiguous in memory.

A numerical library can definitely support constant-time transposition of tensors that returns a view. The one thing a numerical library really shouldn't do is support both constant-time reshaping and slicing on all tensors; the more times you slice and reshape, the more complicated the data layout becomes, increasing the space to store it and time to traverse it.

extra metadata needed to views for different combinations of ops

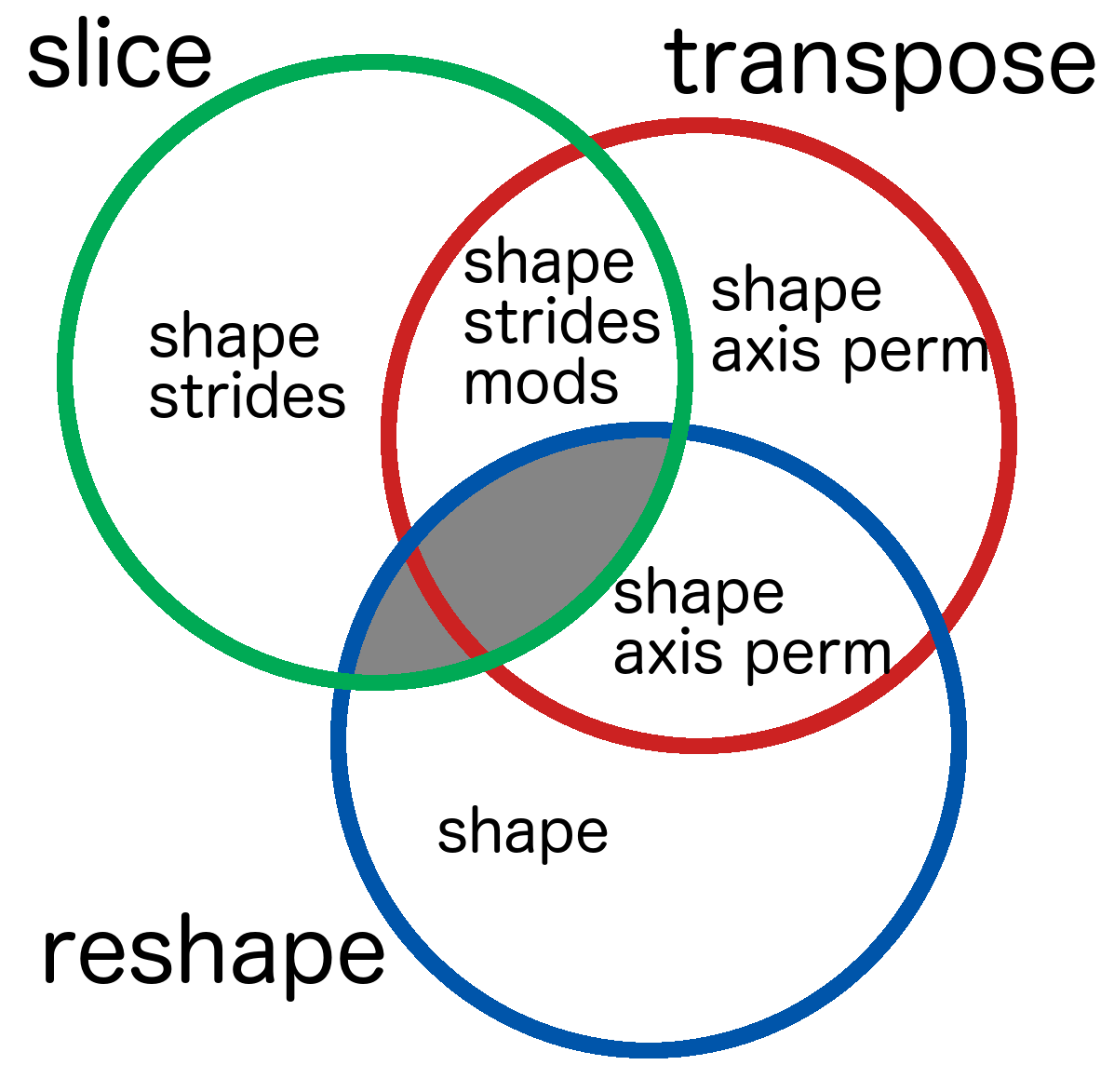
I decided to make numeri return views in constant-time for slices and transposition, but not reshaping. I can do this by further equiping each tensor with strides and mods. Each dimension has a stride, describing how many indices you must go in the data array to get to the next element along that dimension.

For instance, if I have a matrix with strides [100, 10], then to access the [3, 2] element, one needs to go to the 320th element in the data array. Mods support the reverse query - going from index in the array to coordinates. Slicing elements off the start of the tensor can be done by including an offset. Slicing elements off the end can be done by decreasing the shape.

I chose slicing over reshaping because I've found slicing to be much more useful. However, I've noticed that other libraries make different decisions. I'm pretty sure I saw a library that chose reshape and transpose instead of slice and transpose, but I can't find it right now.

Numpy does something very weird. Its slice and reshape operations might return a view, or might not, depending on how complicated the numpy array is. If you slice an array and then reshape it, you will (usually) end up with a copy instead of a view. I'm not a fan of this choice, since it makes output to functions that use numpy unpredictable. If you don't expect to receive a view, you might be surprised to see your original array's data change later on when you modified it in a view. Similarly you might be surprised to see your tensor's values fail to change when you tried to modify what turned out to be a hard copy of it. Plus, views are a bit slower to traverse than if they were contiguous, so numpy's opaque system makes it less obvious how to tune your code for memory or CPU performance.

Code generation for each Tensor

Let's look at two ways to get the loc = [x, y, z] element of a 3D-tensor using strides [100, 10, 1]:

//option A
function get(x, y, z) {
  return this.data[x * 100 + y * 10 + z];
}

//option B
function get(...loc) {
  let idx = 0;
  loc.forEach((coord, dim) => {
    idx += this.strides[dim] * coord;
  });
  return this.data[idx];
}

Option A is massively faster.

• It doesn't have to increment i.
• It doesn't have to check that i is less than the length of loc in the loop.
• It avoids an extra addition to 0.
• It avoids a multiplication of z by 1.

But option A doesn't extend to tensors with arbitrarily many dimensions and arbitrary strides. In JavaScript, I solved this by defining a get function on the tensor at runtime, using its strides. It looks something like this:

const args = Array(n); // for n-dimensional tensor
const terms = [];
if (offset !== 0) {
  terms.push(offset);
}
for (let idx = 0; idx < n; idx++) {
  const arg = `loc${idx}`;
  args[idx] = arg;
  const stride = strides[idx];
  if (stride === 1) {
    terms.push(arg);
  } else if (stride !== 0) {
    terms.push(`${arg}*${stride}`);
  }
}
const formula = terms.join('+');
this.get = new Function(
  ...args,
  `return ${formula}`
);

If you were to read formula, it would be something like loc0*100+loc1*10+loc2. I intelligently come up with the simplest formula. This guarantees the fastest runtime JavaScript can provide.

But getting this to work nicely wasn't trivial. It turns out that defining functions in this way is compute expensive, so I had to invent a clever way to reuse each new Function as much as possible. To be more precise, each new tensor will

1. Compute its formula "case"
2. Check if we've already initialized a tensor of that case
3. If not, dynamically define a curried new Function that returns functions of the desired form, given exact offset and strides (and making sure no one is trying any code injection)
4. Apply this tensor's exact offset and strides to the cached, curried formula

This gives us the best of both worlds: fast tensor initialization and optimal tensor element access.

When can I start using it?

Update

Numeri is stable, and I have used it in multiple cases including Rogue Earth with a good outcome. You can use it today!

While it achieves good performance, is lightweight, and covers a range of use cases that other libraries don't, numeri is still experimental as of this writing. Use it at your own risk. I'm planning a project of my own with it soon.